aba2hom
Introduction¶
This Python script allows the post-processing of thermo-mechanical simulation results obtained using ABAQUS.1 It's purpose is twofold:
Localization of a macroscopic mechanical or thermal state onto a given microstructure¶
It is often desired to transfer a macroscopic state computed at a critical location during the analysis of a part to a known or presumed microstructure, in order to perform a localization analysis, i.e., determine the microscopic fields on the RVE.
The purpose of aba2hom -CritSelect is to support you in this process. It can
-
Print several field results in the Gauss points of all elements of the specified element set. This output can help the user to choose in which element and Gauss point of the macroscale analysis a localization investigation is desired. Stress/strain tensors and their principal values and invariants can be written into an ASCII file
-
Transfer the macroscopic deformation state and the temperature field at the selected critical point to HOMAT in order to perform a localization analysis by applying the macroscopic strains and the mean, macroscopic temperature as boundary conditions on the investigated microstructure.
The computation of effective flow curves from virtual uniaxial tests¶
To assess the mechanical properties of any digital microstucture, the computation of the effective elasto-plastic response is very helpful. Effective flow curves can be obtained from virtual tension/compression experiments.
aba2hom -YieldCurve supports you in the evaluation of such virtual experiments (based on an elestic-plastic Finite Element (FE) simulation in ABAQUS) by
-
Allowing you to specify the time steps (frames in ABAQUS terminology) and quantities to be evaluated.
-
Performing a volume-integration in order to extract effective flow curves (effective equivalent stress \sigma_{\text{eq}}^{\text{eff}} vs. effective equivalent plastic strain \varepsilon_{\text{eq}}^{\text{p,eff}}) or effective stress-strain curves for arbitrary components. Using the default settings, effective equivalent stresses and plastic strains are computed from the corresponding effective tensors, e.g.
\begin{equation} \label{eqn:eqstress} \sigma_{\text{eq}}^{\text{eff}} = \sqrt{\frac{3}{2}\vec{s}^{\text{eff}}:\vec{s}^{\text{eff}}}\,, \end{equation}where \vec{s}^{\text{eff}} is the deviatoric part of the effective stress tensor \vec{\sigma}^{\text{eff}}, which is computed by volume integration of the local quantity
\begin{equation} \vec{\sigma}^{\text{eff}} = \int_{\Omega}\vec{\sigma}(\vec{x})\,\text{d}V\,. \end{equation}
Usage¶
Note that this script only runs in ABAQUS python, i.e., a working ABAQUS setup is mandatory in order to execute it. Assuming that your ABAQUS-command is myabaqus, call aba2hom as
myabaqus python /path/to/aba2hom.py -h
In a real-world scenario, assuming that you are running ABAQUS19 and are in aba2hom's parent directory, this reduces to
abaqus19 python aba2hom.py -h
which prints a help message:
usage: aba2hom.py [-h] (-C | -Y) [-f] [-m] [-o O] cinfile [cinfile ...]
positional arguments:
cinfile Path to the configuration file.
optional arguments:
-h, --help show this help message and exit
-C, -CritSelect Perform CritSelect analysis.
-Y, -YieldCurve Perform YieldCurve analysis.
-f, -FastCalculation Averages the equivalent plastic strain and equivalent
stress over the RVE instead of averaging the
corresponding tensors.
-m, -MatrixOnly Ignore elastic regions.
-o O Basename for the output file.
Options¶
One of the options -C/-CritSelect or -Y/-YieldCurve has to be provided to specify the type of analysis. These options are mutually exclusive.
If -Y/-YieldCurve has been selected, further, rarely used, options are applicable: If -f/-FastCalculation is selected, the effective equivalent stress and strain are obtained by integration the local quantities, i.e.,
This results in a faster calculation; however, this approach is not equivalent to Eq. \eqref{eqn:eqstress}. For proportional loading results obtained using the fast method may be sufficiently accurate. Use with caution.
The -m/-MatrixOnly option excludes elastic parts of your simulation domain (such as hard, elastic particles) from the volume integration. Only use if you know exactly what you are doing.
Output¶
Different output will be produced depending on the selected analysis type. The output filename is based on a BASENAME, which is either derived from the name of the ABAQUS database file (.odb) given in the control file or specified manually using the -o option of aba2hom.
For -C/-CritSelect¶
A BASENAME_crit.txt file is created that contains the header and the requested Gauss point data.
For -Y/-YieldCurve¶
Depending on the output requests (cf. Specific commands of the YieldCurve analysis) in the control file, the following files will be produced:
- For
/SOLUTION, TYPE=YIELD:BASENAME_yield.txtcontaining the problem description and the extracted yield curve for inspection and visualizationBASENAME_yield.matcontaining the yield curve in a format directly readable by ABAQUS
- For
/SOLUTION, TYPE=COMP:BASENAME_stress_strain.txtcontaining the problem description and the requested stress-strain curves
The parameters of the selected analysis are specifies in the input file, which usually has the .cin-extension. The following sections discuss common as well as analysis-specific keywords and options that may appear in this file.
The input file¶
This section describes the structure and syntax of the .cin control files. Each control file contains the keywords described in Sec. Common Section as well as - depending on the type of analysis - either the keywords from Sec. Specific commands of the CritSelect analysis or Sec. Specific commands of the YieldCurve analysis.
Common Section¶
The input file must contain the following keywords followed by one single line with data. The order in which these keywords must appear is not prescribed.
/HEADER_TEXT
The input file starts always with a short comment. This text will appear in the result files. It can be used to describe the selected element set, the macro-scale problem, load case, etc.
/ODB_NAME
Name of the ABAQUS data base to be read.
/INSTANCE
The name of the instance in the ABAQUS model assembly that contains the element set to be considered.
/ELSET
The name of the chosen element set within the ABAQUS model. For -C/-CritSelect Gauss point results from this element set are printed and transferred to the localization analysis within HOMAT. For -Y/-YieldCurve, this is the set from which the yield curve will be extracted; unless you know what you are doing, this set should contain all elements.
Specific commands of the CritSelect analysis¶
The following keywords have to be defined for a -C/-CritSelect analysis. Each keyword expects one line of data.
/STEP
Name of the loading step to be considered for analysis.
/FRAME
Number of the frame (load increment) within the loading step specified in /STEP to be considered.
/FE_MODEL
Type of finite element discretization used in the macro-scale simulation. All supported types are listed in Tab. 1. HOMAT needs this information for further processing the results.
-C/-CritSelect analysis. /FE_MODEL | description |
|---|---|
| 0 | 3-D continuum elements having 6 stess/strain components. This is the default option. |
| 1 | 2-D plane strain/stress and axisymmetric solid elements with 4 strain/stress components.2 |
| 2 | 3-D membrane and shell elements with 3 strain/stress components |
| 3 | axisymmetric shell elements with 2 strain/stress components |
| 4 | truss elements having only 1 axial strain/stress component |
This FE model definition corresponds to the equivalent parameter ABA:MOD in the ASCII transfer file to HOMAT, which specifies in HOMAT the nature of the macro-strain/stress components.
/FIELD
This keyword allows the user to specify the different fields which are selected for printing in the ASCII output file. The identifiers introduced here corresponds to the ABAQUS nomenclature which assures a maximum of compatibility. Mainly the stress/strain tensors, their associated principal values and invariants, like the equivalent von Mises stress, are addressed here. Note that the script distinguishes internally between the tensor fields and the deduced quantities. An overview over the strain-line quantities with the corresponding identifiers is given in Tab. 2.
| identifier | description |
|---|---|
E | linear strain tensor |
LE | logarithmic strain tensor |
NE | nominal strain tensor |
EP | linear principal strains |
LEP | logarithmic principal strains |
NEP | nominal principal strains |
EE | elastic strain tensor |
PE | plastic strain tensor |
CE | creep strain tensor |
IE | inelastic strain tensor |
THE | thermal strain tensor |
EEP | elastic principal strains |
PEP | plastic principal strains |
CEP | creep principal strains |
IEP | inelastic principal strains |
THEP | thermal principal strains |
PEEQ | plastic equivalent strain |
CEEQ | creep equivalent strain |
Note that the accessibility of these quantities depends on their availability in the output database. Correct output requests have to be placed in the STEP-definition of your ABAQUS input file; not all quantities are available in every (thermo-)mechanical analysis, e.g., LE is only available if NLGEOM=ON was specified in your ABAQUS input file. The available stress-like quantities are summarized in Tab. 3.
| identifier | description |
|---|---|
S | true stress tensor |
SP | principal stresses |
MISES | equivalent stress |
PRESS | hydrostatic pressure |
INV3 | 3rd invariant of the stress tensor |
These quantities are computed in every (thermo-)mechanical analysis; however, once again, proper output requests need to be placed in your ABAQUS input file. Other accessible quantities are the strain rates and temperature (cf. Tab. 4).
| identifier | description |
|---|---|
ER | strain rate tensor |
ERP | principal strain rates |
TEMP | the temperature |
The temperature is only available in thermal and thermo-mechanical calculations.
Remark: If the user desires to investigate how each macro-strain component contributes individually to the final critical state on the RVE, he has to edit output file BASENAME_crit.txt and modify it manually. HOMAT searches for the keyword /STRAIN which, by default, corresponds to the total strain tensor. In order to apply only the elastic and thermal strain tensors, the user can change the /STRAIN keyword to /TOTAL STRAIN and the ==/ELASTIC STRAIN or /THERMAL STRAIN into /STRAIN. Thus, the macro-elastic/thermal strains are applied as boundary conditions on the RVE.
Specific commands of the YieldCurve analysis¶
In addition to the described common keywords, the following specific keywords have to be defined for a YieldCurve analysis with Aba2Hom.py.
/FREQUENCY, OPTION = option
This keyword permits the user to specify the time-steps (frames in ABAQUS nomenclature), at which results are read from the ABAQUS data base. Three extraction modes are available and can be selected via the option identifier. The choices are summarized in Tab. 5.
FREQUENCY keyword. option | description |
|---|---|
ALLFRAMES | read results at every time-step (every frame of every loading step) |
FULL_STEP | read results at the end of every loading step (last frame of every loading step) |
DROP | similar to ALLFRAMES, but drops a specified number of frames after every frame read, always includes last frame of every step |
TABLE | read results at manually specified frames |
TABLEX | like TABLE, automatically adds last frame of every step to list |
For OPTION=ALLFRAMES and OPTION=FULL_STEP the /FREQUENCY keyword expects no data lines. For OPTION=TABLE and OPTION=TABLEX at least one line of data is expected; it should conform to the following format:
StepName, Frame#1, Frame#2, .., Frame#n
Here StepName is the name of the selected loading step, such as Step-1, and Frame#1, Frame#2, .., Frame#n are a selection of frame numbers. An example for a valid data line is
Step-1, 1, 6
which selects frames 1 and 6 in Step-1. See Sec. Example for -Y/-YieldCurve for a more comprehensive example.
Advice: The correct selection of time steps has a significant effect on the quality of the extracted curve. You can ensure that you are not missing any potentially crucial part of the curve by selecting OPTION=ALLFRAMES, which however, is the most time-consuming option. For a manual selection of frames it is recommended to consult the .sta file produced by ABAQUS.
/SOLUTION, TYPE = type [, OPTION= option ]
This keyword specifies the effective stress-strain curves to calculate. The parameter type can take the values YIELD, which produces a classical yield curve (effective equivalent stress \sigma_{eq}^{\text{eff}} vs. effective equivalent plastic strain \varepsilon_{eq}^{\text{p,eff}}), and COMP, which produces a stress vs. (total) strain curve for a selected number of components. The selection of stress and strain components for TYPE=COMP is performed using OPTION as described in Tab. 6.
SOLUTION keyword. option | description |
|---|---|
UNIAXIAL | computes \sigma_{ii}^{\text{eff}} vs. \varepsilon_{ii}^{\text{eff}} in the same direction ii in which the virtual test is performed |
LIST | computes \sigma_{ij}^{\text{eff}} vs. \varepsilon_{ij}^{\text{eff}} for specified ij |
RANGE | computes \sigma_{ij}^{\text{eff}} vs. \varepsilon_{ij}^{\text{eff}} for specified ij |
For TYPE=YIELD and TYPE=COMP, OPTION=UNIAXIAL no data lines are required. For the other options one line of data is expected. This line contains a comma-separated list of component numbers (in Voigt notation, cf. Tab. 7) for OPTION=LIST and a range of component numbers for OPTION=RANGE. Examples are:
Ex. 1: Standard yield curve.
/SOLUTION, TYPE=YIELD
Ex. 2: Uniaxial stress-strain curve. The 11 tensor components are extracted.
/SOLUTION, TYPE=COMP, OPTION=UNIAXIAL
Ex. 3: The 11, 33, 23 and 12 components of the stress and strain tensors are extracted.
/SOLUTION, TYPE=COMP, OPTION=LIST
1, 3, 4, 6
Ex. 4: In this last example the range 1, 3 expand to 1, 2, 3, which corresponds to the 11, 22 and 33 components of the stress and strain tensors.
/SOLUTION, TYPE=COMP, OPTION=RANGE
1, 3
Note: The solution keyword can be specified more than once in the input file as illustrated in example Example for -Y/-YieldCurve. This allows the extraction of a yield curve and a number of stress-strain curves in the same run. In this case, the calculated effective curves are all written in a file named PROBLEMNAME_yield.txt.
| indices ij | 11 | 22 | 33 | 12 | 13 | 23 |
|---|---|---|---|---|---|---|
| Voigt component | 1 | 2 | 3 | 4 | 5 | 6 |
Example (.cin) control files¶
Example control files for both supported analysis types are provided below.
Example for -C/-CritSelect¶
In this example the input file for the thermo-elastic plane strain analysis of a sector of the cooled multilayer wall of a gas turbine combustion chamber is outlined (see Fig. 7.1 and paragraph 7.1 of the HOMAT user guide). This example serves as a guide for the present input file description.
As a 2-D plane strain analysis is performed at the macro-scale, FE_MODEL is set to 1 in this example.
/HEADER_TXT
macro-strains extracted in the center of combustion chamber wall
/ODB_NAME
orth_lin.odb
/INSTANCE
MERGED_PART-1
/STEP
Step-1
/FRAME
17
/ELSET
CRIT_TBC+BOND
/FE_MODEL
1
/FIELD
E, S, TEMP, MISES
Example for -Y/-YieldCurve¶
In this example the input file of a YieldCurve analysis corresponding to the uniaxial extension test of the initial austenite microstructure of a FeCMnSi steel alloy is discussed.
/HEADER_TXT
yield curve in X direction of initial austenite microstructure at T=1000C
/ODB_NAME
flow_0s_xx.odb
/INSTANCE
RVE-1
/ELSET
ALL_ELEM
/FREQUENCY, OPTION=TABLE
Step_1, 3, 5, 6, 8
Step_2, 4, 6, 8
Step_3, 2, 4, 5
Step_4, 2, 4, 5
Step_5, 2, 4, 5
Step_6, 2, 4, 5
Step_7, 2, 4, 5
Step_8, 2, 4, 5
/SOLUTION, TYPE=YIELD
/SOLUTION, TYPE=COMP, OPTION=UNIAXIAL
In Fig. 1 the initial austenite microstructure of FeCMnSi steel with 20 randomly oriented grains is shown. The effect of the frequency options (FULL_STEP, ALLFRAMES, TABLE) on the effective yield curve during a uniaxial tensile test in x direction is shown in Fig. 2. As the initial yield stress is derived by extrapolation, the impact of the less accurate option FULL_STEP is significant, while the adopted selection scheme per step predicts an effective elasto-plastic flow curve of same accuracy as the more expensive ALLFRAMES option.
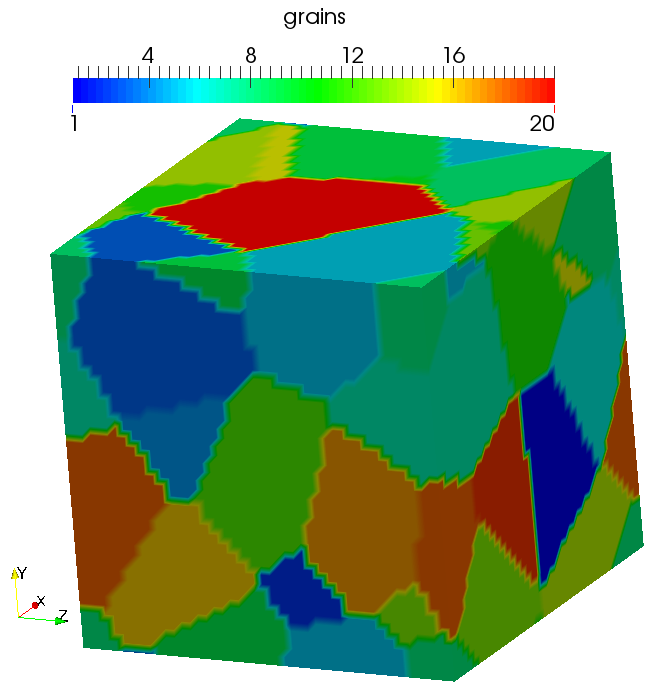
Figure 1: The initial austenite microstructure with 20 randomly oriented grains.
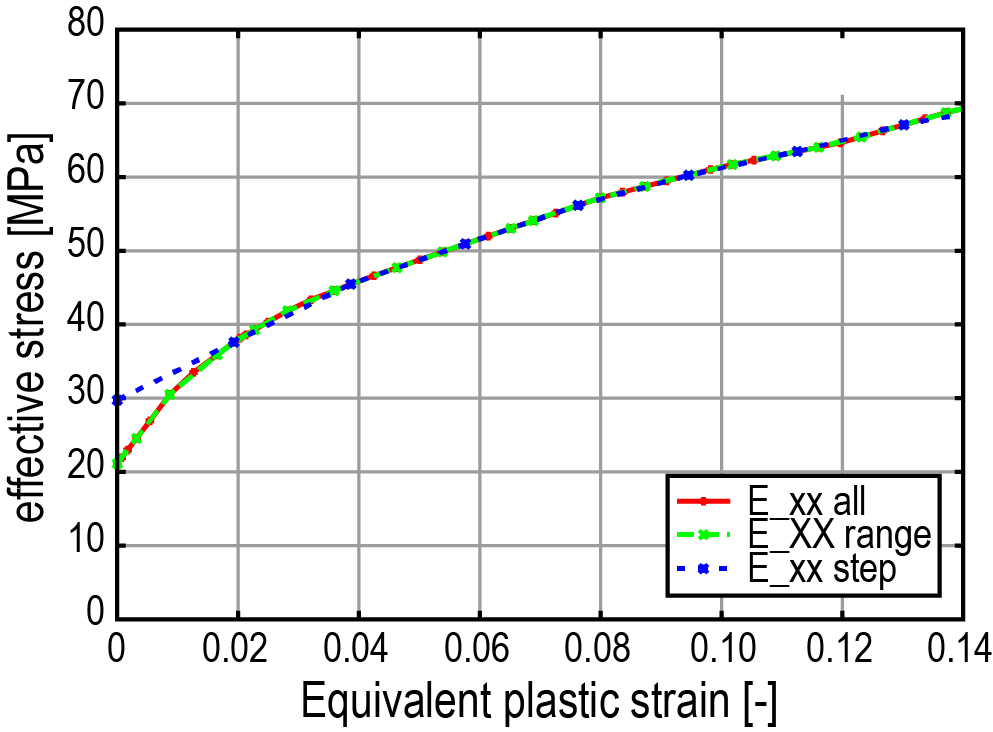
Figure 2: The effective flow curves for an uniaxial tensile test in X direction, evaluated for different selections of local stress/strain results.
-
This version of
aba2homhas been tested with ABAQUS versions 6.13, 6.14, 18 and 19. If you want to apply the script to a database, generated by a version of ABAQUS older than 6.13, please upgrade your database to a more recent version. ↩ -
Note that the third stress/strain component is always set to zero for plane stress elements. ↩