Dendrites¶
The following examples demonstrate how to simulate dendritic solidification of an AlSi7 alloy. The thermodynamics for AlSi7 (liquid and fcc-Al phase) is described as a linearized phase diagram.
One objective is to demonstrate the effects of fluid flow on dendritic growth. This is done by simulating the growth of a dendrite in a forced fluid flow of 1mm/s. MICRESS® currently does not include movement of solid phases, meaning that effects of pressure or frictional forces on solid phases are neglected, so the dendrite is immobile and not transported with the fluid flow.
Figure 1 Dendrite after 15s simulation time
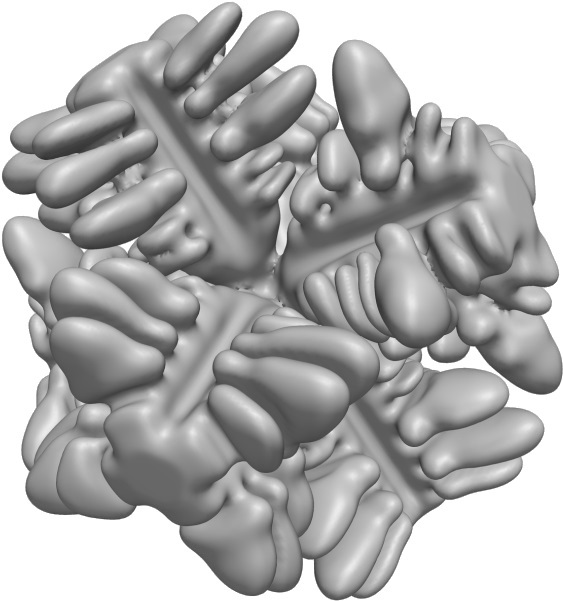
The melt flow affects the local concentration by advective transport. This leads to higher Si concentrations downwind of the solidifying dendrite leading to slower growth in direction of the melt flow. In contrast the dendrite grows faster against the flow direction where the local concentration is lowered due to the oncoming fresh (not Si-enriched) melt. Periodic boundary conditions for the concentration field were employed in the z-direction to keep the total Si-concentration in the simulation domain constant.
Material data for fluid flow is provided by literature: Density of liquid AlSi7 \rho = 2.7 g/cm^3 and the dynamic viscosity at solidification temperatures \mu ≈ 1 \cdot 10^{-3} kg/ms equates to a kinematic viscosity of \nu = \frac{ \mu }{ \rho } = 3.7 \cdot 10^{-3} cm^2/s .
Simulation conditions¶
| Example | A007_Dendrite_AlSi_3D | A008_Dendrite_AlSi_3D_flow |
|---|---|---|
| Dimension | 3-D | |
| Grid size | 100x100x100 cells | 80x80x200 cells |
| Grid spacing | 2 microns | |
| Interface thickness | 3.5 cells | |
| Boundary conditions |
|
|
| Solid phases | fcc_Al | - |
Tweaking performance¶
Since 3D-simulations are computationally intensive, some measures are taken to reduce computation time, especially for fluid flow calculations. The large grid spacing of 2 \mu m is most helpful in this respect, since it reduces the number of simulations cells and allows larger time steps in the flow- and diffusion- parts of the simulation. To avoid deformation of the phase field at the interface on such a coarse lattice, interface stabilisation is employed by supplying an extra parameter for the interfacial energy.
The grid spacing for fluid flow is doubled by means of the flow_coarse option, further reducing the number of simulation cells. The orientation of the dendrite is chosen so that symmetry planes of the cubic anisotropy coincide with symmetric domain boundaries, to reduce the simulation domain.
For the forced fluid flow a fixed velocity in z direction was set at the B and T boundaries. Using a pressure differential would lead to a quickly accelerating flow, especially in the beginning of the simulation when the grain is small and frictional forces are negligible. So an inflow with a fixed velocity was chosen. For the outflow conditions a fixed outflow velocity was chosen for two reasons: Fixing in and outflow velocities leads to faster convergence of the flow solver, also it is more consistent with periodic boundary conditions for the concentration field to match the velocities of the outflow with those of the inflow.
These boundary conditions lead to a uniform velocity of the fluid at the start of the simulation when there is no solid phase. This is determined analytically using the ana_start option. Numerical improvement of the analytical solution is unnecessary and avoided with pre_iter 0. For a rough estimate of the Reynolds number the cross section can be used as a diameter d = 320\mu m.
So in this case piso and combined solver should perform about equally well, this example uses the piso solver. To find optimal values for time stepping tests were done starting with CFL limits C_{adv} = 0.3 and C_{visc} = 0.25 equating to a maximum time step size $\Delta t_{max}.
By observing performance when rising the maximum step size a combination of C_{adv}=0.2 and \Delta t_{max} =5 \cdot 10^{-4} s was found to optimize performance.
To find proper convergence criteria some test runs were made with verbosity 2, observing the convergence at a simulation time when some solid has formed. In this simulation the number of inner and outer piso-cycles is set as limiting element, outer piso cycles were set to 1, inner cycles to 3 after finding that 2 inner cycles were insufficient to reach convergence.
A value of 10^{-2}/s was chosen to limit the continuity error. Pressure and velocity criteria were then adjusted until a sweet spot was found where the accuracy was sufficient and stricter values mainly resulted in more cycles of the linear solvers.
Results¶
Figure 1 shows the simulated dendrite (without flow) at the end of the simulation. In this stage of the simulation growth rate is mostly governed by cooling rate and dendritic ripening can be observed.
In Figure 2 the first 2.5 seconds of the simulation with and without flow are shown side by side. For better comparability the cooling rate in Dendrite_AlSi_3D.dri was changed to -0.1K/s to match that of Dendrite_AlSi_3D_flow.dri. As one can see the advective species transport shifts the concentration in the direction of the melt flow which in turn causes asymmetric growth of the dendrite.
Figure 2 Simulation of dendritic solidification with and without forced melt flow compared side by side. Fluid flow is indicated by arrows, and enhanced concentration is indicated by a dark halo. The dendrite in the melt flow grows faster against and perpendicular to the flow since the Si enriched melt is carried away. In the solute enriched region in flow direction the dendrite grows slowest. Without melt flow the dendrite exhibits only cubic anisotropy, and the Silicon concentration disperses slower.
| t=1 | t=2 |
|---|---|
 |  |
| t=3 | t=4 |
|---|---|
 |  |
| t=5 | |
|---|---|
 |